
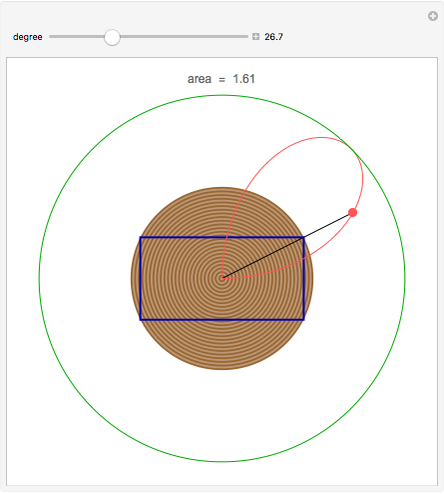
This allowed me to come to the conclusion, using the pythagorean theorem, that the height of the trapezoid is $h=\sqrt. asked in Mathematics by SiaraBasu (94. Find the dimensions of rectangle so that the. I outlined the rectangle within the trapezoid and the two right triangles within it. A rectangle is inscribed in a semi-circle of radius r with one of its sides on diameter of semi-circle. You could do the job just looking at $(0,2)$ but then you have to prove that there isn't any funny stuff going on near either end of the interval that prevents there from being a maximum value.I drew out a circle with a radius of 1 and drew a trapezoid inscribed in the top portion of it. Find the area of the largest rectangle that can be inscribed in a semi-circle of radius r. Find the area of the largest rectangle that can be inscribed in a semi-circle of radius 10. In this case, we only have half of a circle, so we need to modify our circle formula a bit. Note: Inscribed in a semicircle means two vertex of rectangle will located on the circle. Two ways of finding the dimensions/area of the rectangle of maximum area that can be inscribed in a semicircle. Question: Find the area of the largest rectangle that can be inscribed in a semicircle of radius r. The answer is the textbook is A(h)2h times square root of 100-h squared.
#Find area of rectangle inscribed in semicircle how to#
WOW I don't even know how to begin on this one. Find a function that models the area (A) of the rectangle in terms of its Height (H). Well, if that rectangle was bigger than all the other rectangles and the line segments, it's certainly bigger than all the other rectangles, and you have your answer. Find the area of the largest rectangle that can be inscribed in a semi-circle of radius 5. This problem has been solved You'll get a detailed solution from a subject matter expert that helps you learn core concepts. Using this formula we can find the area of this circle inscribed in a rectangle which is inscribed in a semicircle, Area (r2) R/8. Question 1045811: CALCULUS(MAXIMA AND MINIMA):FIND THE MAXIMUM AREA OF A RECTANGLE INSCRIBED IN A SEMI-CIRCLE OF RADIUS 5 INCHES IF ITS BASE LIES ALONG THE. Question 274701: A Rectangle is inscribed in a semicircle of radius 10. And it turns out that this maximum occurs at a value of $x$ that produces a non-degenerate rectangle, not just a line segment. Area of circle piRadius 2 pi (R/2) 2 since the radius of largest circle is R/2 where R is the radius. rects with width now draws the width correctly inside the rects area.
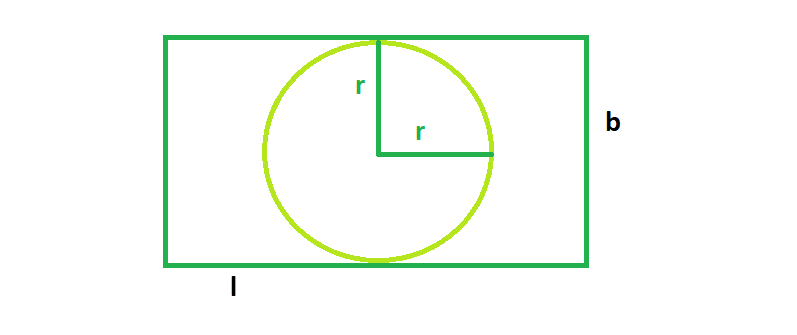
So, if the radius of the semi-circle is R, then the diameter of the largest inscribed circle will be R. The functions return a rectangle representing the bounding area of changed pixels.


A rectangle is inscribed in a semi-circle of radius r with one of its sides on diameter of semi-circle.Find the dimensions of rectangle so that the area is maximum.Find the area. Given a semicircle of radius r, we have to find the largest rectangle that can be inscribed in the semicircle, with base lying on the diameter. And you find the maximum value of $A(x)$ on this entire set. For Largest circle that can be inscribed in this semicircle, the diameter of the circle must be equal to the radius of the semi-circle. A rectangle has two semi-circle described on its longer side as diameter,and the opposite side as tangent.Find the area enclosed between the semi-circles. with no value of $x$ where $A(x)$ matches or exceeds all other values of $A(x).$īut if you decided that instead of looking only at non-degenerate rectangles (the kind that have two dimensions and seem to you to be legitimate rectangles), you will look at this class of shapes that include some line segments (produced when $x=0$ or $x=2$) as well as non-degenerate rectangles.
If you were just doing $x \in (0,2),$ it's conceivable that for some way of generating shapes with that parameter, there's a local maximum at $x = 1,$ but $A(0.1) > A(1),$ $A(0.01) > A(0.1),$ etc. Such examples use closed intervals because as long as $A(x)$ (or whatever you're trying to maximize) is defined everywhere and is continuous on the interval, it has a maximum value in the interval.


 0 kommentar(er)
0 kommentar(er)
